Hidden Gems

Useful Gurobi features you may not know

Matthias Miltenberger

Optimization Support Manager

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Multiple Objectives

Overview

Real-world optimization problems often have multiple, competing objectives:

Maximize Profit

&

Minimize Late Orders

Minimize Shift Count

&

Maximize Worker Satisfaction

Minimize Cost

&

Maximize Product Durability

Maximize Profit

&

Minimize Risk

Multiple Objectives

How does Gurobi handle the trade-offs?

1. Weighted or Blended: Optimize a weighted combination of the individual objectives

flowchart LR
    id1[Obj 1] --- id2[Obj 2] --- id3[Obj 3]

\[ \begin{align*} \min & ~w_1 f_1(x) + w_2 f_2(x) + w_3 f_3(x) \\ \text{s. t. } & ~x \in C \end{align*} \]

2. Hierarchical or Lexicographical: Optimize each objective in a given priority order while limiting the degradation of the higher-priority objectives

flowchart TD
    id1[Obj 1] --> id2[Obj 2] --> id3[Obj 3]

\[ \begin{align*} \min & ~f_1(x) \\ \text{s. t. } & ~x \in C \end{align*} \]

\[ \begin{align*} \min & ~f_2(x) \\ \text{s. t. } & ~x \in C \\ & ~f_1(x) \leq \epsilon_1 \end{align*} \]

\[ \begin{align*} \min & ~f_3(x) \\ \text{s. t. } & ~x \in C \\ & ~f_1(x) \leq \epsilon_1 \\ & ~f_2(x) \leq \epsilon_2 \end{align*} \]

3. Weighted + Hierarchical: Combine both approaches

Multiple Objectives

What does the API look like?

model.setObjectiveN(expr, index, priority=0, weight=1,
                    abstol=1e-6, reltol=0, name="")

# expr (LinExpr): New alternative objective
# index (int): Index for new objective (to set parameters or
#              query solution per objective)
# priority (int, optional): Objective's priority (ObjNPriority attribute)
# weight (float, optional): Objective's weight (ObjNWeight attribute)
# abstol (float, optional): Absolute tolerance used in calculating
#                           allowable degradation (ObjNAbsTol attribute)
# reltol (float, optional): Relative tolerance used in calculating
#                           allowable degradation (ObjNAbsTol attribute)
# name (string, optional): Objective's name

Multiple Objectives

API - Example

Workforce Scheduling:

• First, minimize cost
• Second, make the model “fair”

# Set global sense for ALL objectives
model.ModelSense = GRB.MINIMIZE

# Set up primary objective: minimize total pay cost
model.setObjectiveN(
    gp.quicksum(pay[w] * x[w, s] for w, s in availability),
    index=0,
    priority=2,
    abstol=20,
    reltol=0,
    name="Cost",
)

# Set up secondary objective: minimize difference in shift length
model.setObjectiveN(maxShift - minShift, index=1, priority=1, name="Fairness")

Multiple Objectives

How is the degradation value calculated?

flowchart TD
    id1[Obj 1] --> id2[Obj 2]

additional constraint:

Obj 1 \(\leq\) rhs

\[ \begin{align*} \min & ~f_2(x) \\ \text{s. t. } & ~x \in C \\ & ~f_1(x) \leq \epsilon_1 \end{align*} \]

base_value = max(objbnd + |objval| * MIPGap, objbnd + MIPGapAbs, objval)
relaxation = max(ObjNRelTol * |base_value|, ObjNAbsTol)
rhs(eps_1) = base_value + relaxation

# objbnd    : best bound of objective Obj 1
# objval    : best solution value for objective Obj 1
# MIPGap    : relative MIP gap
# MIPGapAbs : absolute MIP gap
# ObjNRelTol: further allowable relative degradation for Obj 1
# ObjNAbsTol: further allowable absolute degradation for Obj 1

Multiple Objectives

What are the benefits?

• Make the objective functions easy to understand and maintain

• Get faster performance with warm starts for hierarchical objectives

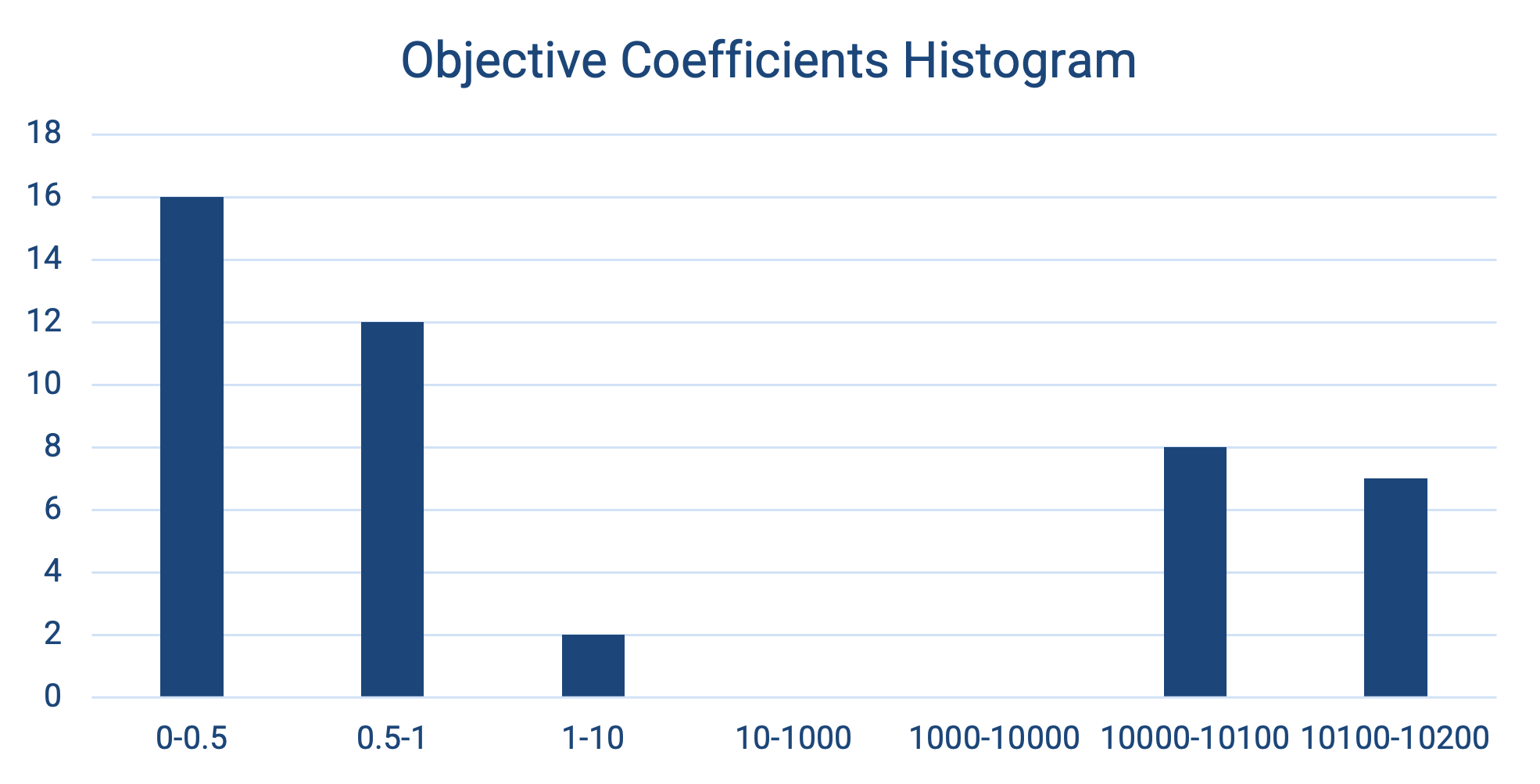
• Avoid numerical issues with large objective coefficients

“There are 45 coefficients in 2 distinct groups.
Is this a multi-objective case in hiding?”

Multiple Objectives

API - Details

• Single objective sense for all objectives controlled via the ModelSense attribute
  • Can always change the sense of individual objectives by multiplying by -1
• Objective expressions must be linear
• Parameters can be set on each objective using multi-objective environments
• Callbacks are available

Too many objectives?

• If your model has too many objectives (more than 10), consider whether you really need them
  • Hierarchical: too many objectives can result in a too small search space
  • Weighted: too many objectives need many groups of distinct, widespread weights, which can result in numerical issues
• Possible alternative: use precedence constraints to model customer priorities

Multiple Objectives

Logging

• Weighted: log will be the same as for a single-objective model

• Hierarchical:

  ---------------------------------------------------------------------------
  Multi-objectives: starting optimization with 3 objectives ...
  ---------------------------------------------------------------------------
  [...]
  ---------------------------------------------------------------------------
  Multi-objectives: optimize objective 1 (Name) ...
  ---------------------------------------------------------------------------

• Mixed:

  ---------------------------------------------------------------------------
  Multi-objectives: starting optimization with 5 objectives (3 combined) ...
  ---------------------------------------------------------------------------
  [...]
  ---------------------------------------------------------------------------
  Multi-objectives: optimize objective 1 (weighted) ...
  ---------------------------------------------------------------------------

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Multiple Scenarios

Modeling What-If?

Idea: One model → solutions to multiple scenarios

Examples:

• “What happens to the optimized production if our forecast is 10% lower than anticipated?”
• “What happens to the building costs if phase 1 is 1 day late? 2 days late? 5 days late?”

Motivation to use the Gurobi Multi-Scenario API:

• Solves faster than separate models
• Easier to maintain and understand

Changes you can make:

• Linear objective function coefficients
• Variable lower and upper bounds
• Linear constraint right-hand-side values

Multiple Scenarios

API - Details

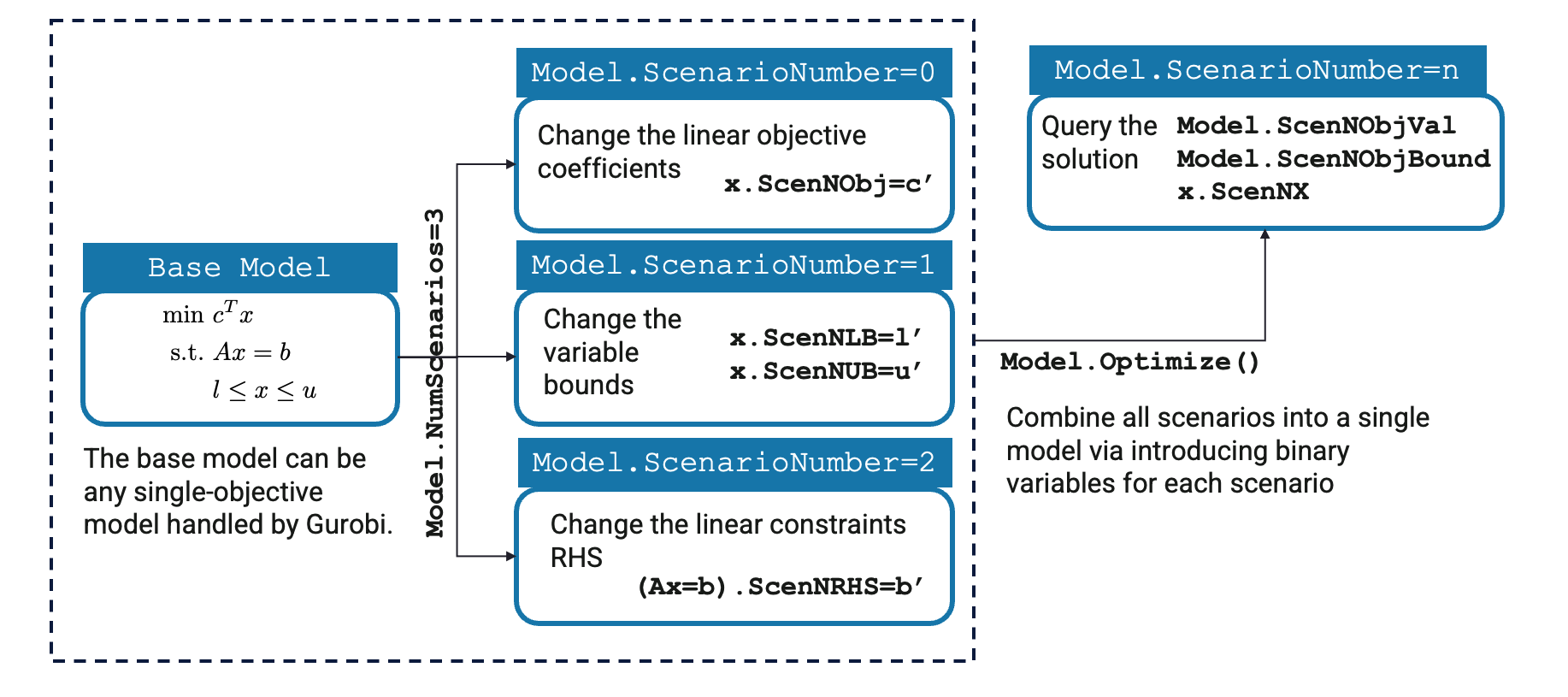
Multiple Scenarios

Tips & Tricks

Multiple scenarios API restrictions

It is not possible to explicitly:

• Add/remove variables or constraints
• Change variable types
• Change the sense of constraints

Tricks to circumvent some restrictions

• To remove a variable, set its bounds to zero
• To add a variable to a scenario, add it to the base with 0 bounds, then change the bounds
• To remove a constraint, change its RHS values to GRB.INFINITY or -GRB.INFINITY
• To add a constraint to a scenario or change its sense, add it as a pair of inequalities to the base model and change its RHS values accordingly

Multiple Scenarios

Logging

Phase 1: Find the best solution over all scenarios

[...]
Solving a multi-scenario model with 2 scenarios...
[...]
    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

H    0     0                    1.850017e+09 8.0000e+08  56.8%     -    0s

Optimal solution found at node 131289 - now completing multiple scenarios...

Phase 2: Find the best solution for each scenario

• Worst Incumbent: The worst solution found over all scenarios
• BestBd: Best possible objective value for any solution that has not yet been found

    Nodes    |    Current Node    |   Scenario Obj. Bounds    |     Work
             |                    |   Worst                   |
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

 1312887 143640 1.5000e+09   58   14 1.5750e+09 1.5000e+09  4.76%   8.5  218s
[...]
Best objective 1.500012833333e+09, best bound 1.500012833333e+09, gap 0.0000%

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Multiple Solutions

General Concept

• Idea: present alternative solutions
  • The model may lack implicit elements like preferences, or some aspects of the objective may be difficult to quantify
  • Demonstrate value by comparing alternatives to the optimal solution
  • Gives a greater feeling of control
  • Get feedback, alternate solution may show missing modeling elements

• How can you quickly report several feasible solutions?
  • Re-run the model with a manually added constraint cutting off the previously reported solution
  • Define a Solution Pool and report multiple solutions automatically after a single run

Subtleties and Limitations

Continuous variables: multiple equivalent solutions will not be reported as per our definitions.

Multiple Solutions

Solution Pool - Setup

Parameter settings	Behavior
PoolSearchMode=0	Stores all solutions found in the regular optimization No additional tree search performed
PoolSearchMode=1 PoolSolutions=n	Stores n-1 additional solutions to the optimal solution Controls how many solutions to save
PoolSearchMode=2 PoolSolutions=n PoolGap=x	Stores n-1 best solutions with a MIPGap less than x% in addition to the optimal solution Requires more expensive tree search than PoolSearchMode=1

# Limit how many solutions to collect
model.setParam(GRB.Param.PoolSolutions, 100)

# Limit the search space by setting a gap for the
# worst possible solution that will be accepted
model.setParam(GRB.Param.PoolGap, 0.10)

# Do a systematic search for the k best solutions
model.setParam(GRB.Param.PoolSearchMode, 2)

Multiple Solutions

Logging

Phase 1: Find one provably optimal solution (identical to MIP log except for last line)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   65.87500    0    1   65.00000   65.87500  1.35%     -    0s

Optimal solution found at node 0 - now completing solution pool...

Phase 2: Populate solution pool

• Worst Incumbent: objective value of the worst solution among the ones in the pool

    Nodes    |    Current Node    |      Pool Obj. Bounds     |     Work
             |                    |   Worst                   |
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   65.00000    0    1          -   65.00000      -     -    0s

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Callbacks

Overview

Idea:

• Monitor the optimization progress
• Modify the behavior of the solver

Examples:

• Add lazy constraints or cuts
• Define custom termination criteria
• Provide additional solutions to the solver

Arguments:

where	from where it is called (Presolve, Simplex, MIP, …)
what	more detailed information about the state of the optimization

Callbacks

Example

import gurobipy as gp

def mycallback(model, where):
  if where == gp.GRB.Callback.MIP:
    solcnt = model.cbGet(gp.GRB.Callback.MIP_SOLCNT)
    nodecnt = model.cbGet(gp.GRB.Callback.MIP_NODCNT)
    if nodecnt >= 10 and solcnt >= 4:
      print('Stop early')
      model.terminate()

model = gp.read("data/glass4.mps")
model.optimize(mycallback)

Callbacks

Example

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
[...]
     0     2 8.0000e+08    0   77 2.0000e+09 8.0000e+08  60.0%     -    0s
H   64    79                    1.950016e+09 8.0000e+08  59.0%  22.5    0s
Stop early
H   74    79                    1.900016e+09 8.0000e+08  57.9%  20.7    0s
[...]
Explored 79 nodes (2138 simplex iterations) in 0.11 seconds (0.08 work units)
[...]
Solution count 5: 1.90002e+09 1.95002e+09 2.00002e+09 ... 3.13336e+09

Solve interrupted
Best objective 1.900016200000e+09, best bound 8.000042222222e+08, gap 57.8949%
User-callback calls 527, time in user-callback 0.00 sec

Callbacks

Remarks

• Inject custom data into the callback before calling optimize() to access it from within:

def mycallback(model, where):
      ...
      if mycallback.value == 1:
        ...

mycallback.value = 1
model.optimize(mycallback)

• Compute Server / Cloud: less frequent and more restrictive

• Can only use methods starting with “cb” (Model.cbGetSolution(), Model.cbSetSolution(), Model.cbLazy(), Model.cbGet()…) and Model.terminate()
• Not possible: adding variables, changing attributes…

Hidden Gems

• Modeling
  • General Constraints
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Infeasibility Analysis

Overview

Gurobi Optimizer version 11.0.3 build v11.0.3rc0 (mac64[arm])
[...]
Optimize a model with 14 rows, 72 columns and 72 nonzeros
[...]

Solved in 0 iterations and 0.00 seconds (0.00 work units)
Infeasible model

Why is the model infeasible?

→ Compute an Irreducible Inconsistent Subsystem (IIS)

What changes do I need to make to recover feasibility?

→ Compute a Feasibility Relaxation

Infeasibility Analysis

Irreducible Inconsistent Subsystem (IIS)

Given an infeasible system of constraints

• Find a subset of constraints and variable bounds that:
  • Is infeasible
  • Removing a single constraint or bound makes it feasible
• IIS is minimal (not minimum)

Meant to be read and analyzed by a human

• The smaller, the better

Computational complexity

• Cheap for LPs and expensive for MIPs

Infeasibility Analysis

Computing an IIS

API

if model.Status == GRB.INFEASIBLE:
    model.computeIIS()
    model.write("iis.ilp")

ILP format

\ Model assignment_copy
\ LP format - for model browsing.
\ Use MPS format to capture full model detail.
Minimize

Subject To
 Thu4: x[Cathy,Thu4] + x[Ed,Thu4] = 4
Bounds
 -infinity <= x[Cathy,Thu4] <= 1
 -infinity <= x[Ed,Thu4] <= 1
End

Control IIS computation

Attributes to include (=1) or exclude (=0) constraints or bounds from the IIS:

IISConstrForce, IISLBForce, IISUBForce, IISSOSForce…

Infeasibility Analysis

Feasibility Relaxation

• Modified model minimizing the amount by which the bounds and linear constraints of the original model are violated

• Violation types (relaxobjtype):

  • Number of violations (0-norm)
  • Sum of the violations (1-norm)
  • Sum of squares of violations (2-norm)

Infeasible model

\[ \begin{align*} \min &~c^T x \\ \text{s. t. } &~Ax \leq b \\ &~x \geq 0 \end{align*} \]

Feasibility relaxation
model

\[ \begin{align*} \min &||(s, u)||_{\color{red}{p}} \\ \text{s. t. } &~Ax -s \leq b \\ &~x + u \geq 0 \\ &~s, u \geq 0 \end{align*} \]

APIs

# Simplified version
model.feasRelaxS(relaxobjtype, minrelax, vrelax, crelax)

# relaxobjtype (integer): 0-norm, 1-norm, 2-norm
# minrelax (boolean): control whether original obj function should be considered
# vrelax (boolean): indicates whether variable bounds can be relaxed
# crelax (boolean): indicates whether constraints can be relaxed

# Full version
model.feasRelax(relaxobjtype, minrelax, vars, lbpen, ubpen, constrs, rhspen)

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Start Features

How to Kickstart your Optimization

• Sometimes Gurobi has trouble finding an initial feasible solution
• This can affect overall performance

Start Values and Variable Hints

→ Complete or partial solutions provided by the user

Start Heuristics

→ Specialized heuristics in Gurobi to produce initial solutions

Start Features

Start Values and Variable Hints

Situation:

• some variables are expected to take a certain value
• (parts) of a feasible solution are known or can be guessed (heuristics, similar model…)

Idea: Reduce solve times by specifying these values

• Start values: to generate an initial feasible solution
• Variable hints: to influence the MIP search

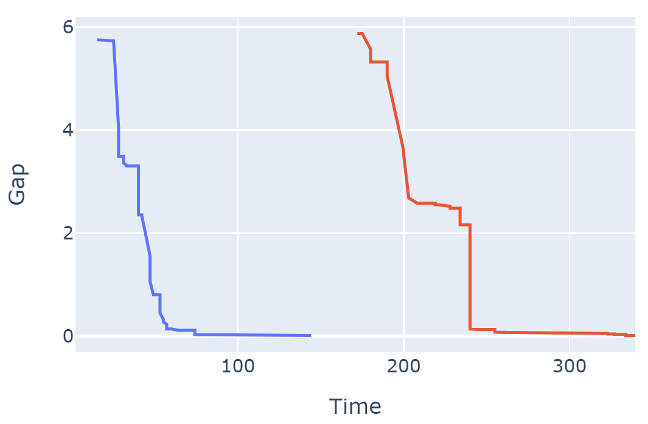
Example: Planning with rolling horizon: every month plan the next 12 months

→ values from prior solution of previous months can be used as start or hints

Start Features

Start Values and Variable Hints - Comparison

Start Values	Variable Hints
Generate initial integer solution, which is improved via MIP search	Guide MIP search toward anticipated values, affects entire solution process
Can specify partial solution, to be completed by solver	Can specify hints for subset of variables, to be used by solver
Use Start variable attribute (or load an .MST MIP start file)	Use VarHintVal variable attribute. Optional confidence by VarHintPri
Supports multiple start values via NumStart model attribute and StartNumber	Supports only one hint per variable

Variables hints and MIP starts are similar in concept, but they behave in very different ways. If you specify a MIP start, the Gurobi MIP solver will try to build a single feasible solution from the provided set of variable values. If you know a solution, you should use a MIP start to provide it to the solver. In contrast, variable hints provide guidance to the MIP solver that affects the entire solution process. If you have a general sense of the likely values for variables, you should provide them through variable hints.

Start Heuristics

No Relaxation Heuristic

• No root LP solution of the full problem required
• Controlled with NoRelHeurTime / NoRelHeurWork parameters
• Runs before optimization to find feasible solutions. When reaching time or work limit, switch to regular branch-and-cut
  • Initially designed for cases where solving the LP is difficult
  • Can help find feasible solutions fast in other cases too

Start Heuristics

Other Start Heuristics (quite expensive, generally poor quality solutions)

• ZeroObjNodes
  • Number of nodes for running the zero objective heuristic
• MinRelNodes
  • Number of nodes for running the minimum relaxation heuristic
• PumpPasses
  • Number of passes of the feasibility pump heuristic

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

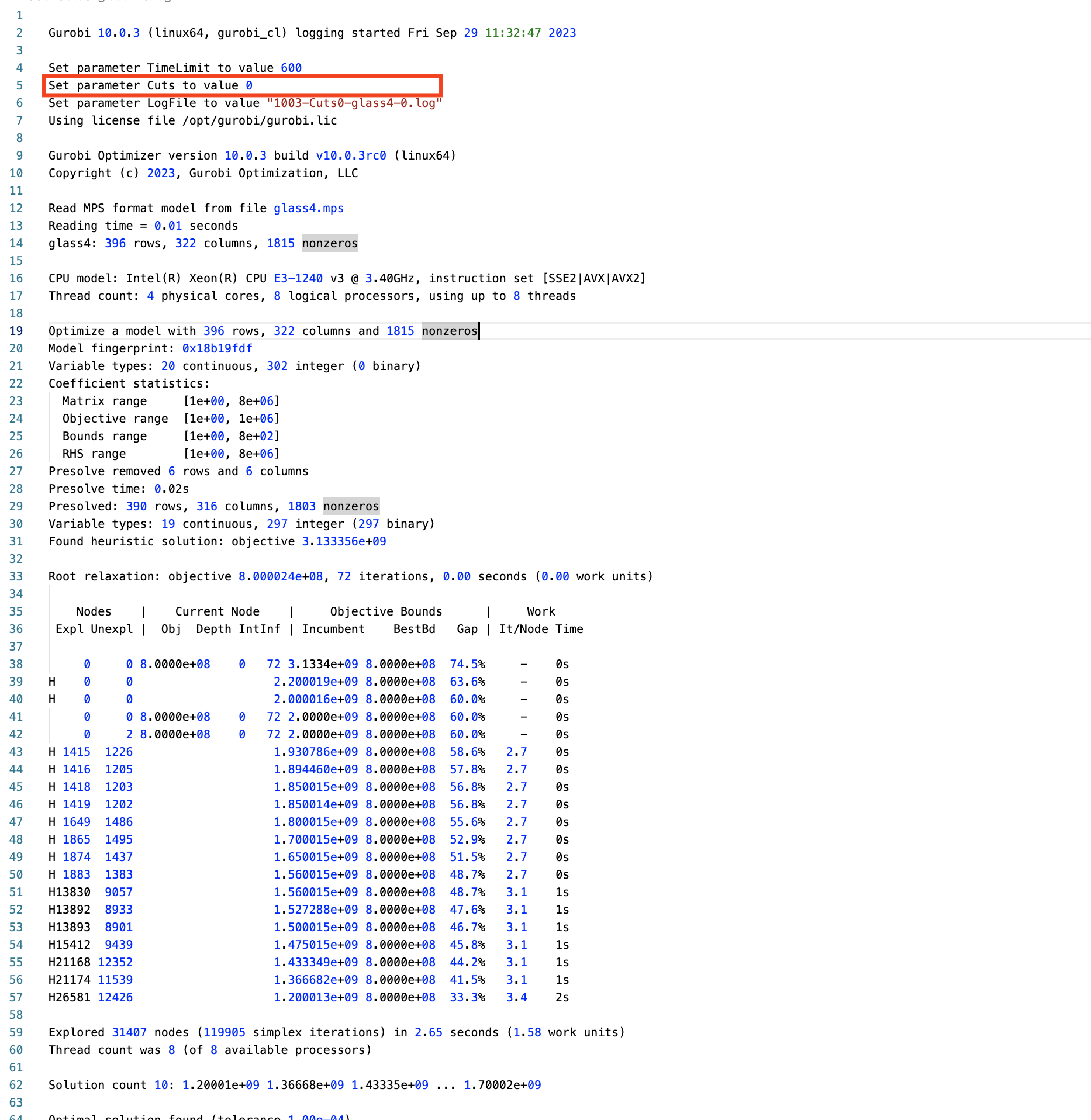
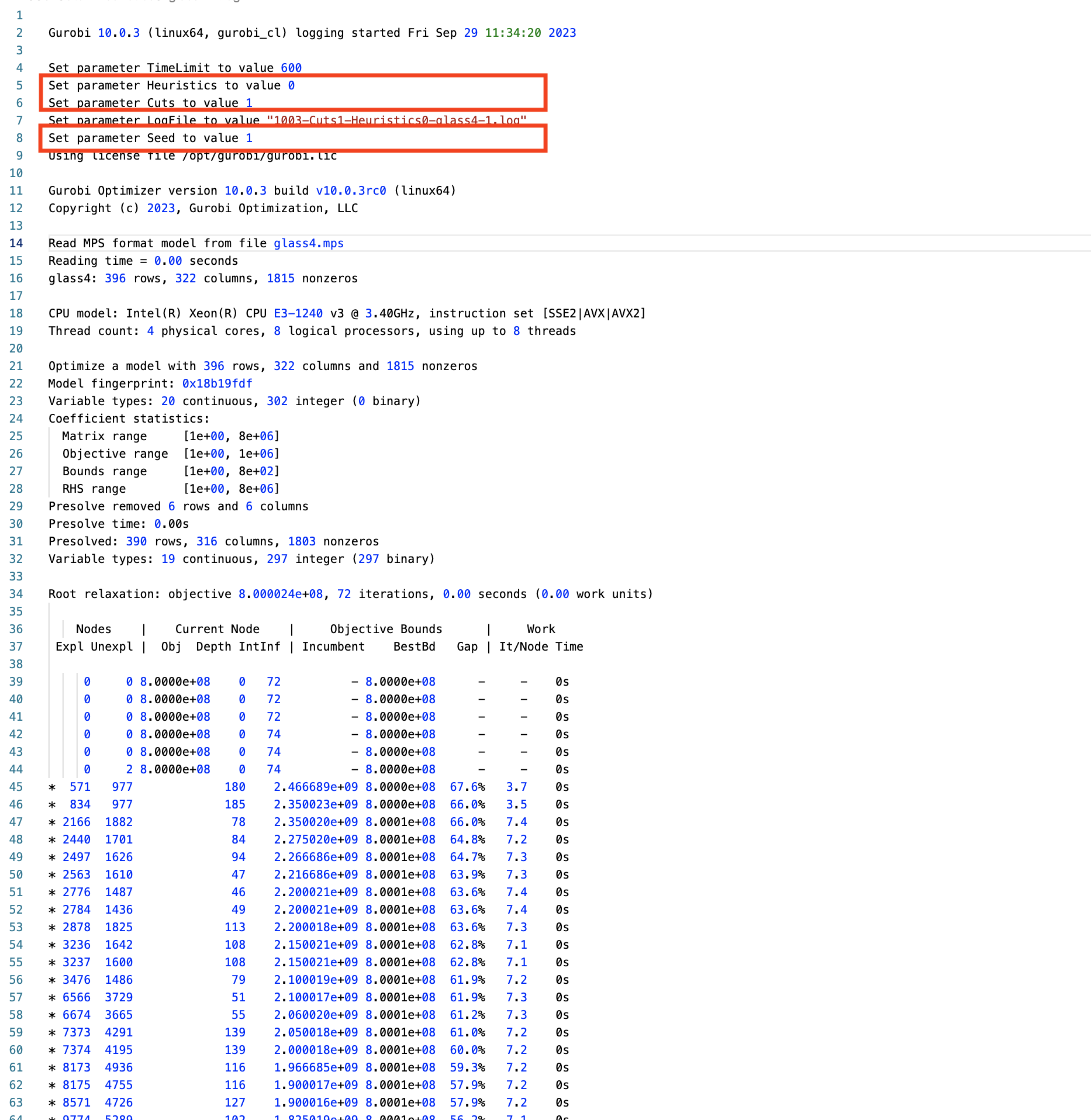
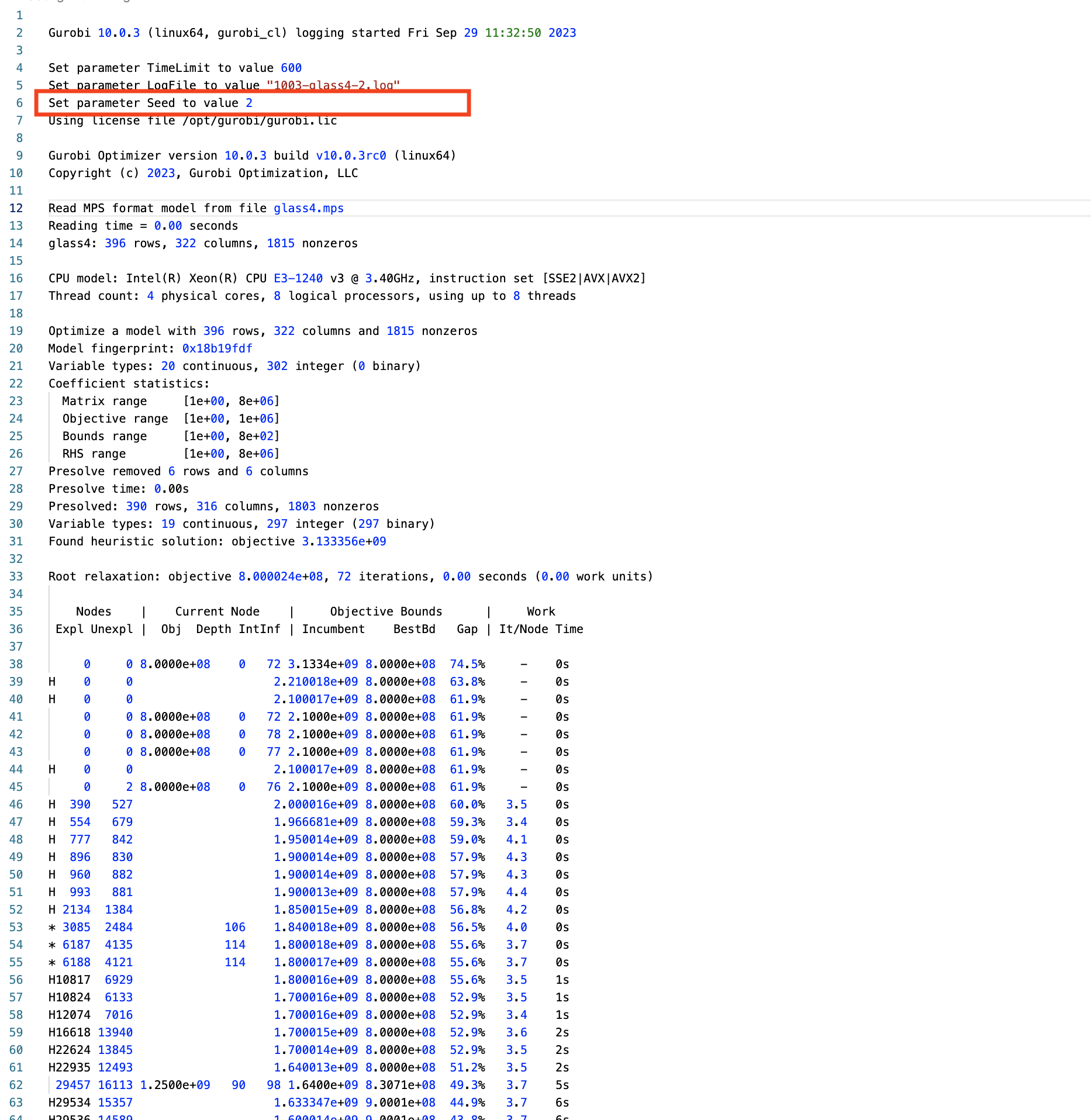
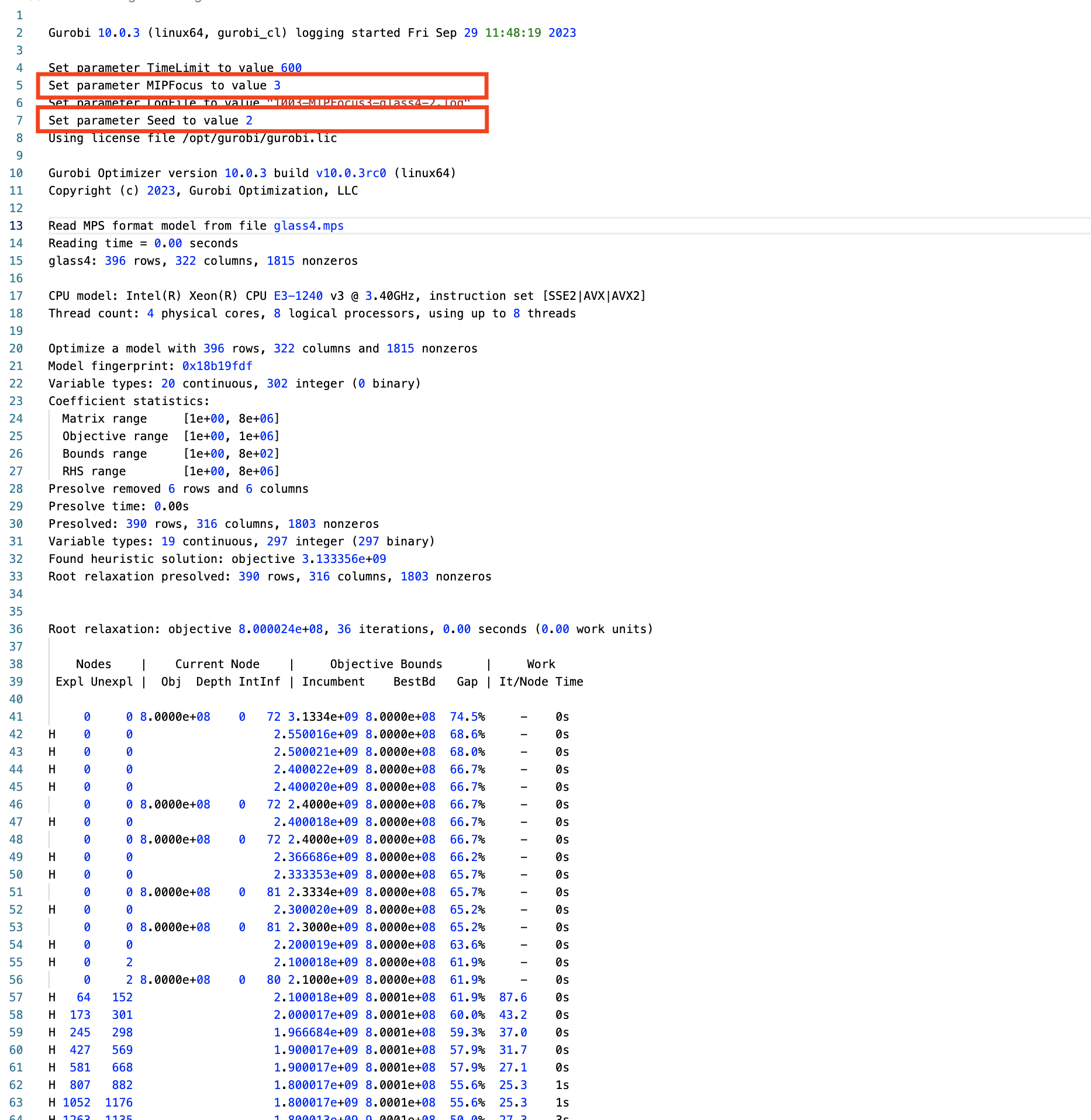
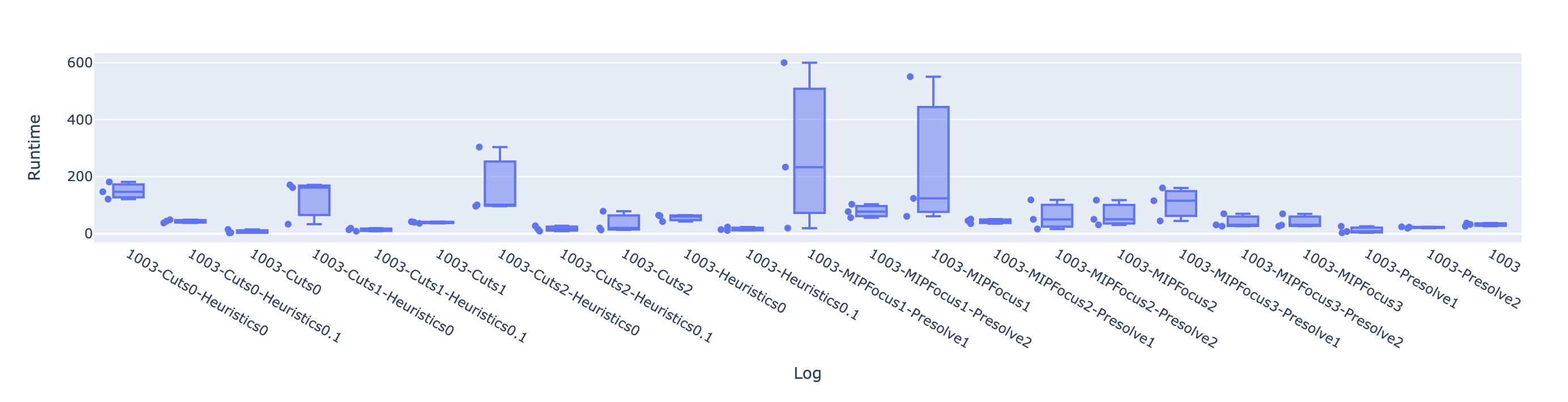
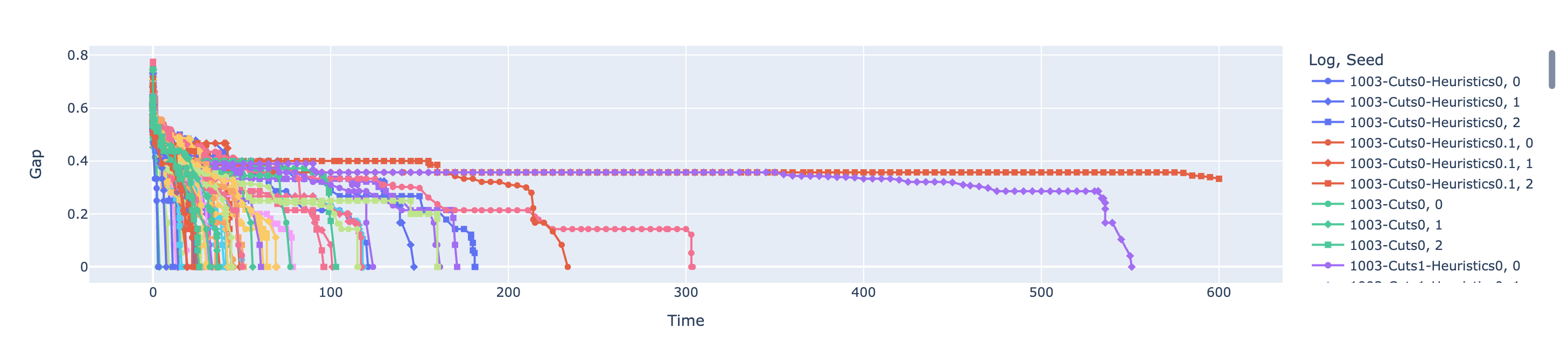
gurobi-logtools

Transform Gurobi logfiles into Pandas DataFrames

• Open-source Python package (github.com/Gurobi/gurobi-logtools)
• Compare different parameter sets, multiple model instances, …
• Interactive visualizations of the aggregated data (runtimes, MIPGap, …)

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

gurobi-modelanalyzer

Numerical model analysis tool and solution checker

• Open-source Python package (github.com/Gurobi/gurobi-modelanalyzer)
• Consists of two main modules:

1. Explainer for ill-conditioned LPs:

• kappa-explain: Provides a row- or column-based ill-conditioning explanation
• angle-explain: Finds pairwise explanations for ill-conditioning

2. Feasibility checks for solution files:

• Why is a given solution infeasible?
• How far is a solution away from feasibility or optimality?

gurobi-modelanalyzer

Quick Start Guide

• Installation: python -m pip install gurobi-modelanalyzer

• Basic usage:

  import gurobipy as gp
  import gurobi_modelanalyzer as gma
  m = gp.read("badmodel.mps")
  m.optimize()
  print(m.kappa)                         # print kappa of final basis
  gma.kappa_explain(m)                   # row-based explanation
  gma.kappa_explain(m, expltype="COLS")  # column-based explanation
  print(gma.angle_explain(m))            # angle explanation

• Modified afiro instance for demonstration:

  Subject To
   R09: - X01 + X02 + X03 = 0
   R09x: - 0.9999999 X01 + X02 + X03 = 0
  [...]

gurobi-modelanalyzer

Output on maliciously modified afiro

• kappa_explain() will generate a new LP or MPS file, containing the ill-conditioning certificate:

  afiro_kappaexplain.lp:

  Minimize
    0 X36 + 0 X04 + 0 X15 + 0 X16 + 0 X26 + 0 X38 + 0 X37
  Subject To
  GRB_Combined_Row: 0.0303868836044176 X23 + 4.80518e-10 X01
    - 4.65661e-10 X03 = 0
  (mult=2696322.968477607)R09x: - 0.9999999000000001 X01 + X03 = 0
  (mult=-2696322.6896988587)R09: - X01 + X03 = 0
  (mult=0.2787787486643817)X46: - X03 + 0.109 X22 <= 0
  (mult=0.030386883604417606)R19: X23 - X22 + X24 + X25 = 0
  (mult=0.030386883604417606)X45: - X25 <= 0
  (mult=0.030386883604417606)X48: 0.301 X01 - X24 <= 0
  Bounds
  End

gurobi-modelanalyzer

Angle Explanation on modified afiro

• angle_explain() returns a list of tuples:
  1. almost parallel rows
  2. almost parallel columns
  3. associated model

  (
    [(<gurobi.Constr R09>, <gurobi.Constr R09x>)],
    [],
    <gurobi.Model Continuous instance basismodel:
      28 constrs, 28 vars, No parameter changes>
  )

This is an “expert” tool that often requires a good understanding of the underlying mathematics to interpret and analyze - just ask our Experts for help!

gurobi-modelanalyzer

Solution checking tool

• Convenient wrapper around feasRelax() and computeIIS()
• Always in relation to the provided solution
• Example using the command-line tool for a feasible solution:

gurobi_solcheck --model examples/data/afiro.mps --sol afiro.json

Objectives:
Fixed:      -459.6919
Optimal:    -464.7531
Difference: -5.0613

• Can also work with infeasible solutions and:
  1. explain why it’s infeasible
  2. repair the solution
  3. repair the model

Hidden Gems

• Modeling
  • Multiple Objectives
  • Multiple Scenarios
  • Multiple Solutions
  • Callbacks
• Analysis and improvements
  • Infeasibility Analysis
  • Start Features
  • gurobi-logtools
  • gurobi-modelanalyzer

Thank you!