graph TD;
root(( ))-->l;
root-->r;
l(( ))-->ll(( )):::green;
classDef green fill:green;
l-->lr(( ));
r(( ))-->rl(( )):::orange;
r-->rr(( )):::orange;
classDef orange fill:orange;
lr-->lrl(( ));
lr-->lrr(( )):::orange;
lrl-->lrll(( )):::orange;
lrl-->lrlr(( )):::orange;
Mastering Numerical Challenges
Gurobi Summit Amsterdam
Introduction
- OR practitioners have to deal with unexpected, counter-intuitive results

- We need an organized approach to deal with the unexpected
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Condition Number
Definition
From \[B(x+\delta x) = b + \delta b \rightarrow \delta x= B^{-1}\delta b\] Cauchy-Schwartz inequalities: \[\|\delta x\| \leq \| B^{-1}\|\|\delta b\|, \|b\| \leq \| B\|\|x\|\] Combine: \[\frac{\|\delta x\|}{\|x\|} \leq \underbrace{\| B\|\| B^{-1}\|}_{\kappa}\frac{\|\delta b\|}{\|b\|}\]
Condition Number
Definition
Definition of condition number \(\kappa\) of a square matrix \(B\) for solving \(Bx=b\)
\(\kappa(B) = \|B\|\cdot\|B^{-1}\|\) provides upper bound on input error amplification in the solution of a linear system \(Bx=b\). It is the normed reciprocal of the distance to singularity.
- Effect of the input error \(\delta b\) on the output error \(\delta x\):

\[ \frac{\|\delta x\|}{\|x\|} \leq \kappa(B) \cdot \frac{\|\delta b\|}{\|b\|} \]

- Example: Error of \(10^{-16}\) in the input \(b\) and \(\kappa \approx 10^{10}\) can cause error up to \(10^{-6}\) in \(x\)
Double precision
Default feasibility tolerance
Condition Number
Value Range
\(\kappa\) :
\(\;1 \dots 10^7\)
stable
\(\;10^7 \dots 10^{10}\)
suspicious
\(\;10^{10} \dots 10^{14}\)
unstable
\(\;>10^{14}\)
ill-posed
Note
Condition number always represents an upper bound or worst-case scenario!
Condition Number
Interpretations
Linear Algebra Interpretation
- How linearly dependent hyperplanes are.
- Rows are linearly dependent if and only if \(B\) is singular, or any columns (rows) are linearly dependent.
- How close \(B\) is to being singular
Geometrical interpretation
The condition number is the ratio between two circles: the smallest circle enclosing the feasible region and the largest circle enclosed by the feasible region
Condition Number
Geometrical interpretation
Which system of equations do you think will have a better condition number?
A: 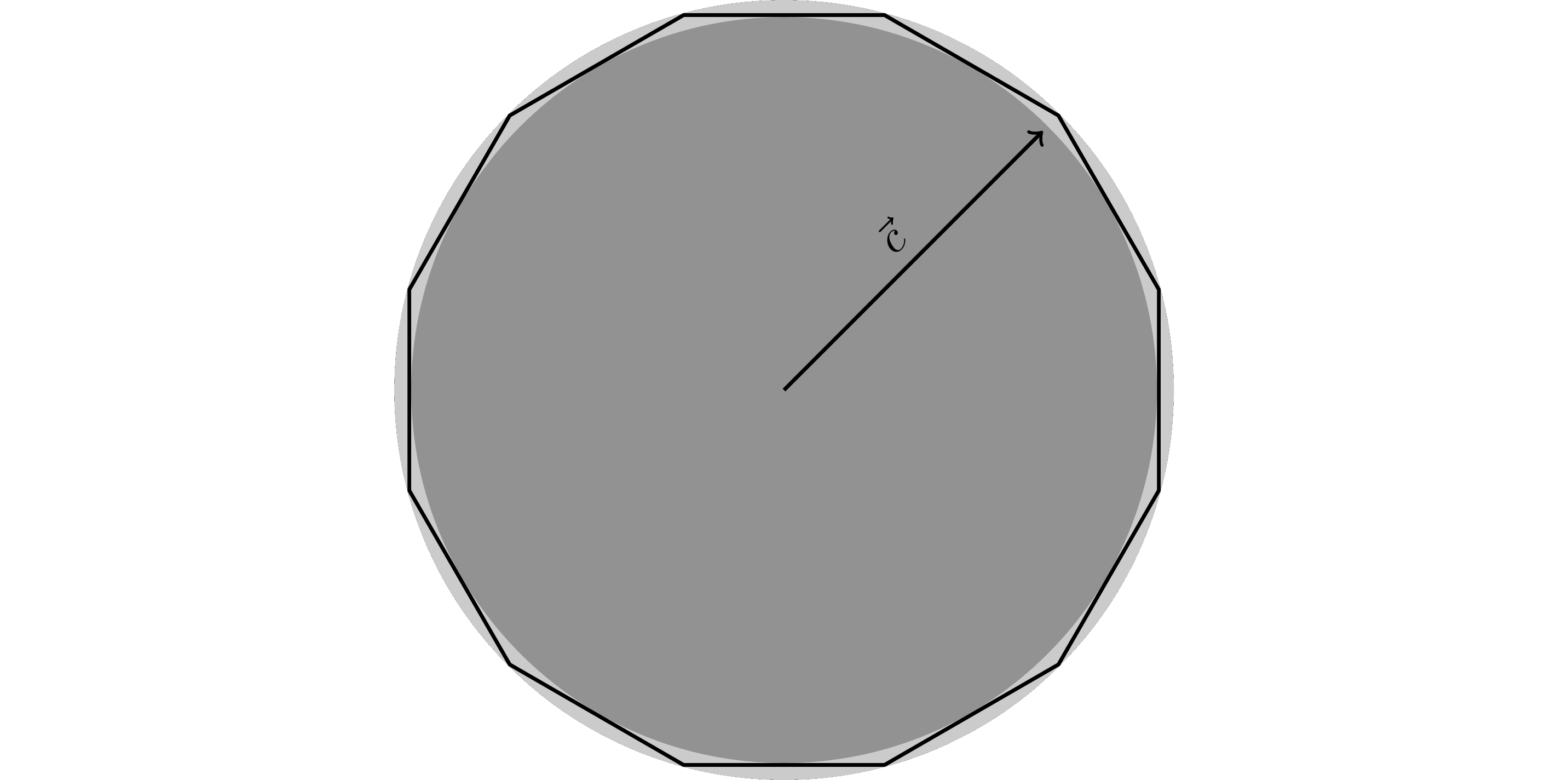
B: 
Example 1
Large matrix coefficient ranges
\[
\begin{align}
& B=\begin{pmatrix}
M & 1\\
0 & \frac{1}{M} \end{pmatrix}
\text{ has inverse }
B^{-1}=\begin{pmatrix}
\frac{1}{M} & -1\\
0 & M \end{pmatrix}\\
& \Rightarrow \|B\| \geq M \text{ and } \|B^{-1}\| \geq M\\
& \Rightarrow \kappa(B) = \|B\|\cdot\|B^{-1}\| \color{red}{\geq M^2}
\end{align}
\]
- Avoid unnecessarily large
big Mvalues - Avoid unnecessarily small units of measurement
- Avoid combining both of these!
Example 1.2
Large matrix coefficient ranges
What would happen if we replace \(\frac{1}{M}\) with just \(M\)?
\[ \begin{align} & B=\begin{pmatrix} M & 1\\ 0 & M \end{pmatrix} \text{ has inverse } B^{-1}=? \end{align} \]
The inverse would become: \[ B^{-1}=\begin{pmatrix} \frac{1}{M} & \frac{-1}{M^2}\\ 0 & \frac{1}{M} \end{pmatrix}\Rightarrow \|B^{-1}\|\geq \frac{1}{M} \Rightarrow \kappa(B) \geq 1 \]
Example 2
Inconsistent or unnecessarily truncated data
- Values that should be equal have small differences
- Example:
c306: 0.416666667 x80 – 100 x90 = 0 [...] c11360: 0.416666666 x80 – 100 x90 = 0
- Values appear to be calculated inconsistently
- Values are only calculated to 9 digits → bigger perturbation than necessary

Example 3
Hidden mixtures of large and small coefficients
- \(\kappa(B)=\|B\|\cdot\|B^{-1}\|\) is large if \(\|B\|\) or \(\|B^{-1}\|\) is large
- \(\|B^{-1}\|\) can also be large for other reasons
- Cascade or staircase: \[ B=\begin{pmatrix} 1 & -2 & & & \\ & 1 & -2 & & \\ & & \ddots & \ddots & \\ & & & 1 & -2 \\ & & & & 1 \\ \end{pmatrix} ,\; B^{-1}=\begin{pmatrix} 1 & 2 & 4 &\dots & 2^{n-1} \\ & 1 & 2 & \dots & 2^{n-2} \\ & & \ddots & \ddots & \vdots \\ & & & 1 & 2 \\ & & & & 1 \\ \end{pmatrix} \]

Quick summary
Reasons for a high condition number
- Large spread of coefficients
- Strange properties (e.g. cascade)
- Almost linear dependent rows or columns
How can we fix this?
Important
The condition number is a property of the problem! Not the solution process.
Probably reformulation but wait and see!
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Why is this relevant?
LPs
A solution to an LP requires:
- A basis
- Feasibility verification or proof of infeasibility
- Optimality verification or proof of unboundedness
Requires solving two linear systems of equations (with basis matrix \(B\)):
- Primal solution: \(\ \;x_B=B^{-1}(b-A_N x_N)\)
- Dual solution: \(\quad\pi^T = c_B^T B^{-1}\)
Why is this relevant?
LPs
In the simplex algorithm, large condition numbers may lead to:
- Incorrect selection of pivots due to numerical errors.
- Pivots not found due to numerical errors.
- Excessive iterations.

For verification, \(B\) is used.
Why is this relevant?
LPs
- A stable implementation tries to avoid running into badly conditioned bases along the way
- Steepest edge pricing and Harris ratio test (Bixby and Rothberg, 2003).
- Markowitz tolerance in basis factorization
- May not always be possible
Why is this relevant?
MIPs
- The LP relaxation is solved after every branching decision and cut.
- Pruning, optimality checks (these are hard!).
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Floating Point Numbers
Fails basic mathematical properties:
- Commutativity
- Associativity
Floating Point Numbers
Fails others: Commutativity in multiplication
Representation of Numbers
| type | # of bits | mantissa | exponent | arch |
|---|---|---|---|---|
float |
32 | 23 | 8 | most |
double |
64 | 52 | 11 | most |
long double |
80 | 63 | 15 | e.g. x86-64 (intel or AMD) |
long double |
128 | 112 | 15 | e.g. Power 9 |
Representation of Numbers
float representation of 1234.5 (calculator)
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Analyzing
- Solution and Formulation
- Optimization
- Different runs
Analyzing
Solution & Formulation
- Model statistics:
model.printStats() - Solution quality:
model.printQuality()- Many more Quality Attributes
- Check the condition number.
- We will see how later…
Analyzing
Optimization
Warning
Look out for warnings!
Prior to optimization 🚩
Optimize a model with 306204 rows, 579547 columns and 1563587 nonzeros
Model fingerprint: 0x21cdd0c7
Coefficient statistics:
Matrix range [1e-05, 2e+08]
Objective range [8e-370, 1e+05]
Bounds range [1e-03, 3e+09]
RHS range [5e-01, 2e+04]
Warning: Model contains large matrix coefficient range
Warning: Model contains large bounds
Consider reformulating model or setting NumericFocus
parameter to avoid numerical issues.Analyzing
Optimization
During LP solving (simplex or barrier) 2x🚩
Iteration Objective Primal Inf. Dual Inf. Time
[...]
56658 -3.3179831e+03 4.239720e+05 0.000000e+00 20s
Warning: Markowitz tolerance tightened to 0.0625
67557 -3.2801023e+03 1.974011e+04 0.000000e+00 25s 69517 3.7944349e+02 6.207667e+04 0.000000e+00 30s
Warning: 1 variables dropped from basis
Warning: switch to quad precision
78320 1.7027054e+08 1.149199e+04 0.000000e+00 35sAnalyzing
Optimization
During the MIP node process 🚩
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
[...]
3252 0 278173.332 0 2120 275179.027 277183.668 0.73% 211 401s
3253 0 278173.020 0 2060 275179.027 277115.904 0.70% 211 405s
Relaxation Markowitz Tolerance tightened to 0.5
3254 0 278173.020 0 2060 275179.027 277115.904 0.70% 211 406s
[...]
3575 295 postponed 43 275179.027 277115.904 0.70% 321 461s
3599 314 infeasible 44 275179.027 277115.904 0.70% 332 467s
3673 391 276640.457 55 1881 275179.027 277115.904 0.70% 328 471spostponed nodes may have to be processed later - but hopefully never. Many of these in quick succession is 3x🚩
Analyzing
Optimization
Post Optimization 3x🚩
Solved in 131511 iterations and 75.99 seconds (66.11 work units)
Optimal objective 1.730551793e+08
Warning: unscaled dual violation = 0.0141201 and residual = 0.0111682- This can also be checked with the quality attributes or
MaxVio. Checkout other Quality Attributes.
Analyzing different runs
Important
Numerical issues can lead to different solutions!
- What happens if we run the same model using different seeds?
- Does the solution remain the same?
- Does the time remain similar?
- This may be due to other factors
- Ranging between: 🚩 - 3x🚩 (small difference in runtime - feasible for some seeds, infeasible for others)
Analyzing different runs
Two different solutions for harp2 (using MIPGap=0).
Model Reformulation
The problem with big-M
import gurobipy as gp
M = 1e10
opts = {"OutputFlag": 0}
with gp.Env(params=opts) as env, gp.Model(env=env) as m:
c = m.addVar(name="c", lb=0)
b = m.addVar(name="b", vtype=gp.GRB.BINARY)
# Fix variables
c.UB = 1e4
c.LB = 1e4
b.UB = 1e-6 # This is technically zero based on the IntFeasTol
b.LB = 1e-6
m.addConstr(c <= M*b) # So we really want c = 0 since b = 0
m.optimize()
print(f"Is the model optimal? {m.Status==gp.GRB.OPTIMAL}")Is the model optimal? TrueHow can we fix this?
Model Reformulation
Alternative 1: Using indicator constraints
import gurobipy as gp
M = 1e10
opts = {"OutputFlag": 0}
with gp.Env(params=opts) as env, gp.Model(env=env) as m:
c = m.addVar(name="c", lb=0)
b = m.addVar(name="b", vtype=gp.GRB.BINARY)
# Fix variables
c.UB = 1e4
c.LB = 1e4
b.UB = 1e-6 # This is technically zero based on the IntFeasTol
b.LB = 1e-6
m.addConstr((b == 0) >> (c == 0))
m.optimize()
print(f"Is the model optimal? {m.Status==gp.GRB.OPTIMAL}")Is the model optimal? FalseModel Reformulation
Alternative 2: Tighten IntFeasTol
import gurobipy as gp
M = 1e10
opts = {"OutputFlag": 0, "IntFeasTol": 1e-7}
with gp.Env(params=opts) as env, gp.Model(env=env) as m:
c = m.addVar(name="c", lb=0)
b = m.addVar(name="b", vtype=gp.GRB.BINARY)
# Fix variables
c.UB = 1e4
c.LB = 1e4
b.UB = 1e-6 # This is technically zero based on the IntFeasTol
b.LB = 1e-6
m.addConstr(c <= M*b) # So we really want c = 0 since b = 0
m.optimize()
print(f"Is the model optimal? {m.Status==gp.GRB.OPTIMAL}")Is the model optimal? FalseAgenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
There are many parameters

… and choosing the right ones is no easy task
Parameter recommendations
NumericFocus = [0, 1, 2, 3]
Meta parameter that affects many aspects of the solution process:
Presolve
- Tighter tolerances when fixing variables
- Avoid small coefficients in bound strengthening
- More restrictive checks in aggregator
Root relaxation
- Simplex
- Tighten MarkowitzTol tolerance
- Use Quad precision
- Barrier
- More conservative step sizes
Cuts
- Only rank-1 MIR Cuts
- Less aggregation
- Disable Gomory Cuts for
>= 2 - Disable all Cuts for
= 3
Parameter recommendations
Presolve = [-1, 0, 1, 2]
Presolve typically makes numerically challenging models worse.
The main culprits are:
Aggregate- may introduce accumulation of numerical errors- Try setting this to
0to deactivate aggregation
- Try setting this to
Parameter recommendations
Root relaxation or pure LP: Simplex
- MarkowitzTol: pivoting tolerance (for LU factorization)
- Larger values increase numerical stability at the expense of sparsity
Remember the warning:
Iteration Objective Primal Inf. Dual Inf. Time
[....]
56658 -3.3179831e+03 4.239720e+05 0.000000e+00 20s
Warning: Markowitz tolerance tightened to 0.0625
[....]- Gurobi dynamically adjusts this to balance performance and stability
Try setting it to the displayed value right from the start!
Parameter recommendations
Root relaxation or pure LP: Simplex
Quad = [-1, 0, 1]- Higher precision at the expense of speed and memory
-1switches dynamically to quadruple precision if numerical issues arise
Parameter recommendations
Root relaxation or pure LP: Barrier
BarHomogeneous = [-1, 0, 1]- Default or homogeneous algorithm
- Homogeneous algorithm is usually a bit slower
- Homogeneous is better in recognizing infeasibility or unboundedness, or dealing with models that are at the boundary of infeasibility
Crossover = [-1, ..., 4]- Helps clean up numerical dirt (e.g. small violations)
- Consider turning it off (
0) if it stalls, or even settingQuadto1this can help!
Parameter recommendations
MIP
Cuts = [-1, ..., 3]0: Disable all cuts (together withCutPasses = 0to be completely shut off, may affect heuristics, so I do not recommend this)1: Moderate cut generation2, 3: Aggressive and even more aggressive
GomoryPasses- Most numerically sensitive cutting planes
- Dense (degrades the LP stability)
- Uses a row of the basis matrix inverse and requires solving another system of linear equations (risking further issues)
- Most numerically sensitive cutting planes
Parameter recommendations
MIP
IntegralityFocus = [0, 1]- Enables extra computations to avoid trickle flow (like in the big-M example)
- Generate a “cleaner” solution with fewer tiny solution values
- Typically safe to enable but may be expensive
Parameter recommendations
SOS and general constaints
General constraints are reformulated to a mix of linear and SOS1/2 constraints (SOS2 are only used for PWL approximations).
PreSOS1BigM = 0to turn off the linearisation (which uses Big-M values) and use them in branching.- (+) more numerically stable, (-) worse relaxation
Parameter recommendations
MIQCP
PreMIQCPForm = [0, 1, 2]set to 0 to turn off any reformulation and handle them in brancem in branchingg- (+) more numerically stable, (-) potentially harms performance
Parameter recommendations
MINLP
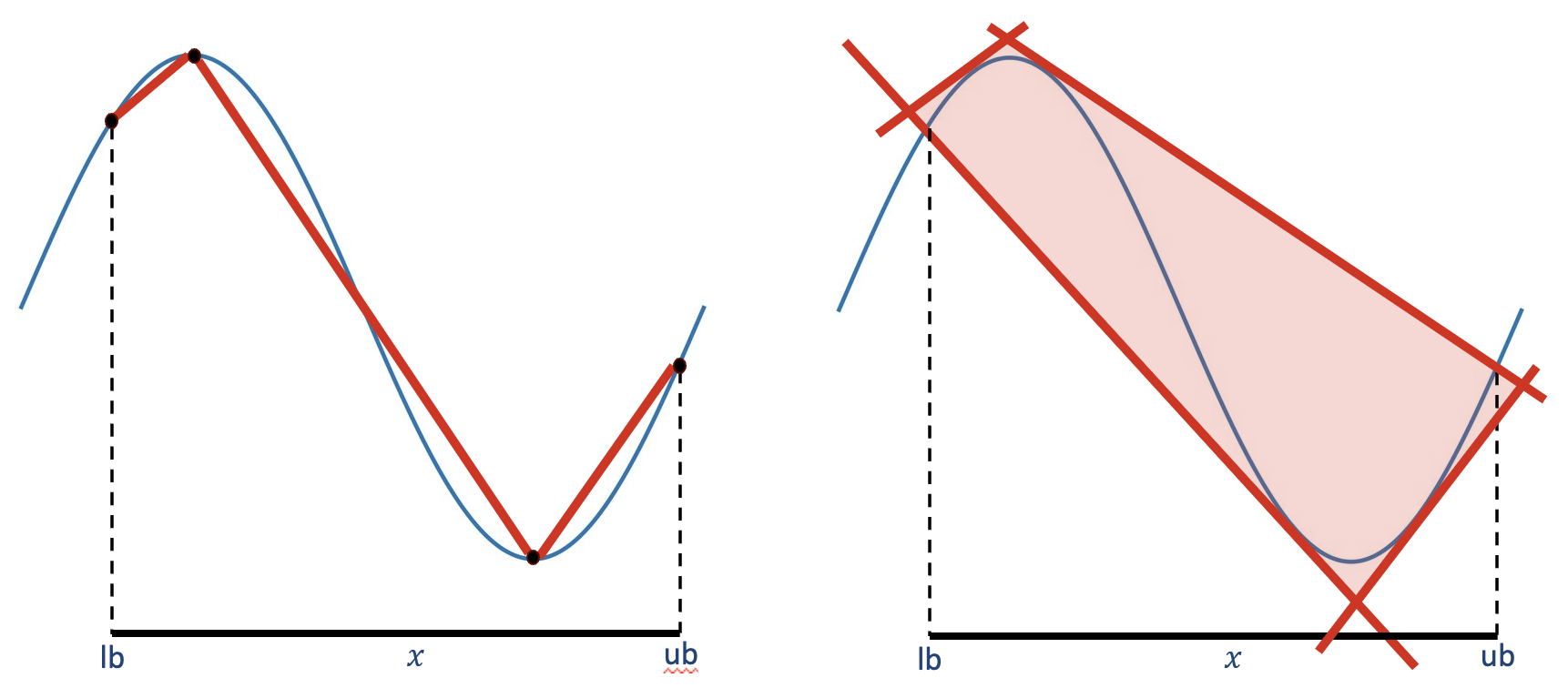
FuncNonlinear = [0, 1]- Use outer approximation instead of piecewise-linear approximation
- More accuracy, potentially more expensive
- When enabled, parameters
FuncPieces,FuncPieceError,FuncPieceLength,FuncPieceRatioare obsolete - Only available from Gurobi 11. From version 12 the default is 1.
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Practical recommendations:
Summary
Analyze:
- Solutions
- Logs
- Different runs
Warning
Don’t ignore the warnings!
Model instance:
- Coefficient statistics
- Can the ranges be reduced?
- Is presolve helping?
Mathematical formulation:
- Is there an alternative way of formulating the problem?
Practical recommendations:
Summary
Warning
Turn to parameter tuning only after model improvements have been investigated!
- Try stabilizing the solving behavior via different parameters
- Run multiple seeds and slight variations of the model
Tip
Contact the Gurobi Experts team for assistance!
Agenda
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Short intermission: FeasRelax
Modified model minimizing the amount by which the bounds and linear constraints of the original model are violated
Violation can be measured as:
- Number of violations (0-norm)
- Sum of the violations (1-norm)
- Sum of squares of violations (2-norm)
Infeasible model
\[ \begin{align*} \min &~c^T x \\ \text{s. t. } &~Ax \leq b \\ &~x \geq 0 \end{align*} \]
Feasibility relaxation
\[ \begin{align*} \min &||(s, u)||_p \\ \text{s. t. } &~Ax -s \leq b \\ &~x + u \geq 0 \\ &~s, u \geq 0 \end{align*} \]
Tip
Also very helpful to investigate why a model is infeasible!
Basic idea
Approximiate the distance to singularity
Apply FeasRelax to minimize the sum of infeasibilities of:
\[ \begin{align} B^Ty = 0 \\ e^Ty = 1 \\ y \; \text{free} \end{align} \]
- Rows of \(B\) with very small \(y\) component are filtered out
- Support of \(y\) provides a row-based certificate of the ill-conditioning
- Add constraint \(e^Ty=1\) to prevent \(y=0\)
\[ \begin{align} By = 0 \\ e^Ty = 1 \\ y \; \text{free} \end{align} \]
- Columns of \(B\) with very small \(y\) component are filtered out
- Support of \(y\) provides a column-based certificate of the ill-conditioning
Third case: Examine angles of pairs of matrix rows and columns
- Vectors \(u\) and \(v\) are almost parallel if \(u^Tv - \|u\|\cdot\|v\| < \epsilon\).
Challenges
- The FeasRelax problem is an LP whose structural columns comprise an ill-conditioned basis matrix
- Set
NumericFocus=3andScaleFlag=2if row and column ratios are large - Provide more custom parameters via
PRMfile
- Set
- Too many rows or columns in the output; hard to determine source of ill-conditioning
- Try different explanation method (row, column, angle)
- Sometimes one method provides a much smaller explanation
Quick Start Guide
- Installation:
python -m pip install gurobi-modelanalyzer
Basic usage:
Quick Start Guide
Modified
afiroinstance for demonstration:
Output on maliciously modified afiro
kappa_explain()will generate a new LP or MPS file, containing the ill-conditioning certificate:afiro_kappaexplain.lp:
Minimize
0 X36 + 0 X04 + 0 X15 + 0 X16 + 0 X26 + 0 X38 + 0 X37
Subject To
GRB_Combined_Row: 0.0303868836044176 X23 + 4.80518e-10 X01
- 4.65661e-10 X03 = 0
(mult=2696322.968477607)R09x: - 0.9999999000000001 X01 + X03 = 0
(mult=-2696322.6896988587)R09: - X01 + X03 = 0
(mult=0.2787787486643817)X46: - X03 + 0.109 X22 <= 0
(mult=0.030386883604417606)R19: X23 - X22 + X24 + X25 = 0
(mult=0.030386883604417606)X45: - X25 <= 0
(mult=0.030386883604417606)X48: 0.301 X01 - X24 <= 0
Bounds
EndAngle explanation on modified afiro instance
angle_explain()returns a list of tuples:- almost parallel rows
- almost parallel columns
- associated model
“Real” example: neos-1603965 (MIPLIB 2017)
- Use
model.relax()to relax integrality conditions - Final condition number
1.60000000016e+21(original model) angle_explain()does not reveal any almost parallel rows or columns
Subject To
GRB_Combined_Row: = 1.000000015655
(mult=0.999999999815)R24991: C8008 - C8009 >= 0
(mult=9.9999999981499e-11)R9004: - 1e+10 C8008 <= 0
(mult=9.9999999981499e-11)R13004: - 0.15 C7002 + 1e+10 C8009 <= 1e+10
(mult=1.4999999997225e-11)R1030: C3030 - C7001 <= 0
(mult=-1.4999999997225e-11)R1966: C3966 - C7001 <= 0
(mult=-1.4999999997225e-11)R2966: C4966 - C7002 <= 0
(mult=-1.4999999997225e-11)R28014: C0030 + C3030 = 7165
(mult=1.4999999997225e-11)R28950: C0966 + C3966 + C4966 = 8221
(mult=1.12499999982e-11)R0030: 1.3333333333 C0030 = 0
(mult=-1.12499999982e-11)R0966: 1.3333333333 C0966 = 0- Don’t ignore rows with small \(y\):
big-Mvalues of \(10^{10}\) are the issue here
More functionality
Solution Checker
Test and diagnose a solution for your model e.g.
- Your solution is feasible but possibly suboptimal
- Your solution is infeasible and:
- You want an explanation why it’s infeasible
- You want to repair the solution
- You want to repair the model
More functionality
Solution Checker
import gurobipy as gp
import gurobi_modelanalyzer as gma
m = gp.read("glass4.mps")
sol = {m.getVarByName("x1"): 600, m.getVarByName("x22"): 0}
sc = gma.SolCheck(m)
sc.test_sol(sol)
print(f"Solution Status: {sc.Status}")More functionality
Solution Checker
sc.optimize()
for v in sol.keys():
print(f"{v.VarName}: Fixed value: {sol[v]}, Computed value: {v.X}")(even) More functionality
converttofractions():- takes a list of decimal values and tries to represent them as fractions
- useful to clean-up “dirty” coefficients
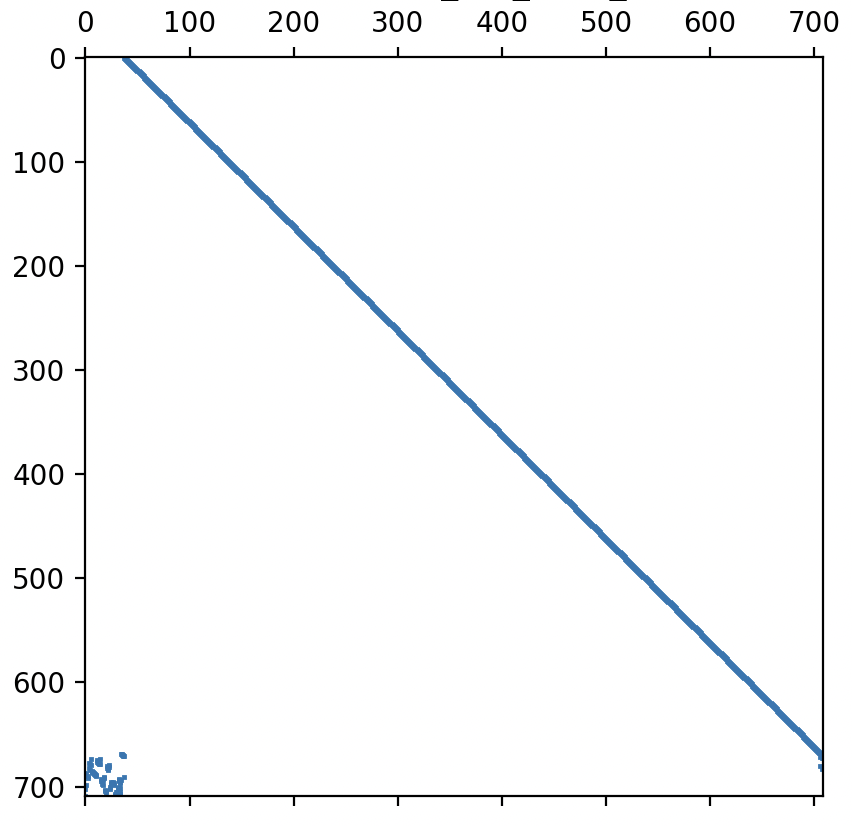
matrix_bitmap():- wrapper for
spy()(matplotlib) to inspect sparsity pattern - useful to identify cascades
- wrapper for
Summary
Track down reasons for numerical issues
Open-source (Apache-2.0) on GitHub:
Install via pip:
python -m pip install gurobi-modelanalyzerCurrently only supports LPs (use
model.relax()to inspect root LP of MIPs)
Get involved and share your feedback and ideas!
Thank You!
www.gurobi.com
Questions? Comments?
Remarks?
- Concept
- Condition number
- Why is this relevant?
- Floating point numbers
- Practical recommendations
- Analyzing
- Parameters
- Summary
- Ill-Conditioning Explainer
Further Material
- Klotz, E. (2014). Identification, assessment, and correction of ill-conditioning and numerical instability in linear and integer programs. In Bridging Data and Decisions (pp. 54-108). INFORMS.
- Gurobi Tech Talk: Converting Weak to Strong MIP Formulations, YouTube, Materials.
- Gurobi Holiday Tech Talk: Prevent the Grinch from Stealing Your Optimization Projects, YouTube, Materials.
©️ Gurobi Optimization